Research

Quantum many-body systems away from equilibrium

Foundations of statistical mechanics

• understanding the behavior of macroscopic systems from the laws of quantum mechanics, which describe the motion and interactions of their microscopic constituents
• equilibration: systems approach a macroscopically stationary state
• thermalization: the stationary state can be characterized by thermodynamic ensembles (microcanonical, canonical, ...)

Universality of thermalization and exceptions

• eigenstate thermalization hypothesis (ETH) as the presumed mechanism for thermalization, but unproven
• violations of the (strong) ETH in systems with an extensive number of conserved quantities ("integrable systems") and in other special cases
• weaker versions of the ETH provable for certain classes of systems, e.g., if the Hamiltonian is translationally invariant
• weak ETH ensures thermalization for local nonequilibrium initial conditions

Relaxation processes

• many-body systems prepared away from equilibrium generically relax and approach a (thermal) equilibrium state
• effect of small-to-moderate perturbations on the relaxation: prethermalization, a typicality theory for the observable dynamics and its refinements

Driven systems

• time-dependent forcing to drive systems away from equilibrium
• if heating is slow, response strongly suppressed near thermal equilibrium under peridic driving (compared to effects away from equilibrium under otherwise identical circumstances)
• effective time reversal ("echo protocols") to probe irreversibility
• persistence of echo signals in many-body quantum systems (as opposed to classical systems)

Stochastic thermodynamics and active matter

Mesoscopic scales

• nano- to micrometer-sized systems
• examples: macromolecules, proteins, suspended colloids, bacteria
• no quantum effects, but strong thermal fluctuations
• stochastic dynamical systems (described by Langevin/Fokker-Planck equations)

Snapshot of a system of active particles exhibiting motility-induced phase separation: Particles cluster in some regions of the accessible volume, while other regions maintain a dilute, gas-like appearance, even though particle interactions are purely repulsive.

Stochastic thermodynamics

• extension of thermodynamic concepts (heat, entropy, efficiency, ...) to systems with strong fluctuations and far away from equilibrium
• analyzing heat engines and their efficiency at mesoscopic scales
• fluctuation theorem for and thermodynamic interpretation of irreversibility in active matter systems

Active matter

• suspensions of mesoscopic active particles: particles can consume energy from their environment to propel themselves forward persistently
• examples: bacteria, colloids with catalytic surfaces, nanorobots
• inherently out of equilibrium due to constant energy conversion
• numerous intriguing collective phenomena (e.g., motility-induced phase separation)
• irreversibility of the observable dynamics, its intuitive understanding and its relation to thermodynamics

Statistical physics of and with machine-learning models

Machine-learning models as complex systems

• large number of elementary units
• relatively simple "microscopic laws" for their interactions
• complex "macroscopic" behavior emerging from the interplay of the elementary units
• training algorithms formulated as equations of motion for the model degrees of freedom with the goal to minimize an objective function

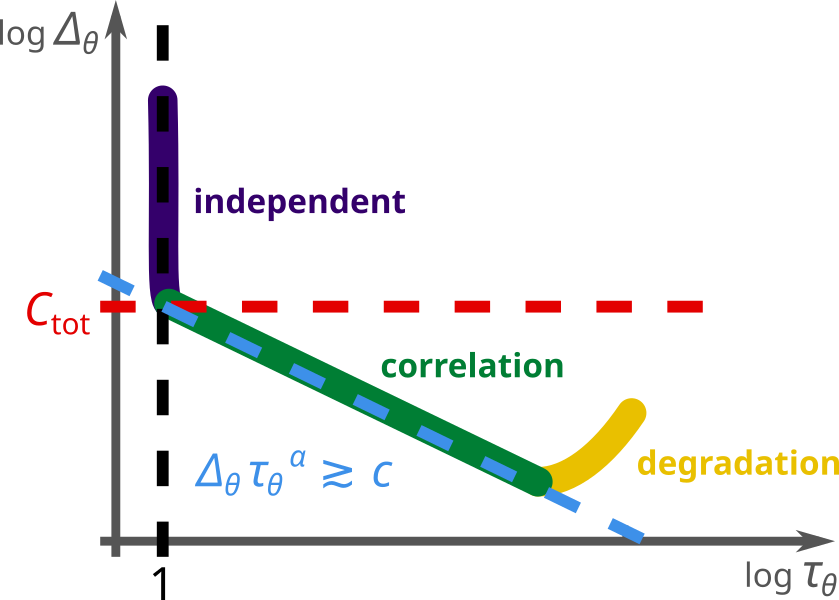Sketch of the three learning regimes and accuracy-efficiency tradeoff of RBMs. The regimes are characterized by the models divergence Δ_θ from the target distribution ("accuracy", the smaller the better) and its integrated autocorrelation time τ_θ ("efficiency", the smaller the better).

Restricted Boltzmann Machines

• unsupervised machine-learning model
• idea: find an optimal representation of an unknown target probability distribution within a family of Boltzmann distributions
• particulary popular in physics applications, akin to a spin glass
• learned model distribution can be used to generate new samples or analyze other (approximate) properties of the target
• largely universal learning characteristic with three regimes (independent learning, correlation learning, and degradation) and a tradeoff between the model's accuracy and sampling efficiency

Publications

Preprints

• LD and P. Reimann,
  Random-matrix approach to time-dependent forcing in many-body quantum systems,
  arXiv:2409.10052
• LD and M. Ueda,
  Symbolic equation solving via reinforcement learning,
  arXiv:2401.13447
• LD and R. Eichhorn,
  Thermodynamic nature of irreversibility in active matter,
  arXiv:2308.03625

Peer-reviewed research articles

1. LD and P. Reimann,
   Stalled response near thermal equilibrium in periodically driven systems,
   Nat. Commun. 15, 294 (2024)
2. LD and M. Ueda,
   Three learning stages and accuracy-efficiency tradeoff of Restricted Boltzmann Machines,
   Nat. Commun. 13, 5474 (2022)
3. LD, P. Vorndamme, and P. Reimann,
   Thermalization of locally perturbed many-body quantum systems,
   Phys. Rev. B 105, 024310 (2022)
4. P. Reimann and LD,
   Refining Deutsch's approach to thermalization,
   Phys. Rev. E 103, 022119 (2021)
5. LD and P. Reimann,
   Typical relaxation of perturbed quantum many-body systems,
   J. Stat. Mech. 2021, 013106 (2021)
6. LD, S. Bo, and R. Eichhorn,
   How irreversible are steady-state trajectories of a trapped active particle?',
   J. Stat. Mech. 2021, 033216 (2021)
7. LD and R. Eichhorn,
   Irreversibility in active matter: General framework for active Ornstein-Uhlenbeck particles,
   Front. Phys. 8, 582992 (2021)
8. LD, P. Vorndamme, and P. Reimann,
   Modification of quantum many-body relaxation by perturbations exhibiting a banded matrix structure,
   Phys. Rev. Research 2, 033210 (2020)
9. LD and P. Reimann,
   Persistent many-body quantum echoes,
   Phys. Rev. Research 2, 023216 (2020)
10. LD and P. Reimann,
    Predicting imperfect echo dynamics in many-body quantum systems,
    Z. Naturforsch. A 75, 403 (2020)
11. LD and P. Reimann,
    Relaxation theory for perturbed many-body quantum systems versus numerics and experiment,
    Phys. Rev. Lett. 124, 120602 (2020)
12. LD, H. Gies, and B. Knorr,
    Momentum dependence of quantum critical Dirac systems,
    Phys. Rev. D 99, 125019 (2019)
13. LD, S. Bo, and R. Eichhorn,
    Irreversibility in active matter systems: fluctuation theorem and mutual information,
    Phys. Rev. X 9, 021009 (2019)
14. S. Manikandan, LD, R. Eichhorn, and S. Krishnamurthy,
    Efficiency fluctuations in microscopic machines,
    Phys. Rev. Lett. 122, 140601 (2019)
15. P. Reimann and LD,
    Typicality of prethermalization,
    Phys. Rev. Lett. 122, 080603 (2019)
16. A. Argun, J. Soni, LD, S. Bo, G. Pesce, R. Eichhorn, and G. Volpe,
    Experimental realization of a minimal microscopic heat engine,
    Phys. Rev. E 96, 052106 (2017)

Dissertation

• LD,
  Predicting quantum many-body dynamics out of equilibrium,
  PhD Thesis, Bielefeld University (2021)

Teaching